April 15th, 2018 • Comments Off on Agent based bidding for merging graphs
There are multiple ways to merge two stitch two graphs together. Next to calculating all possible solutions or use evolutionarty algorithms bidding is a possible way.
The nodes in the container, just like in a Multi-Agent System [1], pursue a certain self-interest, as well as an interest to be able to stitch the request collectively. Using a english auction (This could be flipped to a dutch one as well) concept the nodes in the container bid on the node in the request, and hence eventually express a interest in for a stitch. By bidding credits the nodes in the container can hide their actually capabilities, capacities and just express as interest in the form of a value. The more intelligence is implemented in the node, the better it can calculate it’s bids.
The algorithm starts by traversing the container graph and each node calculates it’s bids. During traversal the current assignments and bids from other nodes are ‘gossiped’ along. The amount of credits bid, depends on if the node in the request graph matches the type requirement and how well the stitch fits. The nodes in the container need to base their bids on the bids of their surrounding environment (especially in cases in which the same, diff, share, nshare conditions are used). Hence they not only need to know about the current assignments, but also the neighbours bids.
For the simple lg and lt conditions, the larger the delta between what the node in the request graphs asks for (through the conditions) and what the node in the container offers, the higher the bid is. Whenever a current bid for a request node’s stitch to the container is higher than the current assignment, the same is updated. In the case of conditions that express that nodes in the request need to be stitched to the same or different container node, the credits are calculated based on the container node’s knowledge about other bids, and what is currently assigned. Should a pair of request node be stitched – with the diff conditions in place – the current container node will increase it’s bid by 50%, if one is already assigned somewhere else. Does the current container node know about a bid from another node, it will increase it’s bid by 25%.
For example a container with nodes A, B, C, D needs to be stitched to a request of nodes X, Y. For X, Y there is a share filter defined – which either A & B, or C & D can fulfill. The following diagram shows this:
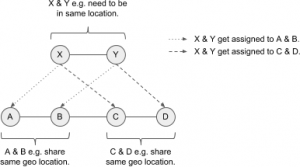
(Click to enlarge)
Let’s assume A bids 5 credits for X, and B bids 2 credits for Y, and C bids 4 credits for X and D bids 6 credits for Y. Hence the group C & D would be the better fit. When evaluating D, D needs to know X is currently assigned to A – but also needs to know the bid of C so is can increase it’s bid on Y. When C is revisited it can increase it’s bid given D has Y assigned. As soon as the nodes A & B are revisited they will eventually drop their bids, as they now know C & D can serve the request X, Y better. They hence sacrifice their bis for the needs of the greater good. So the fact sth is assigned to a neighbour matters more then the bid of the neighbour (increase by 50%) – but still, the knowledge of the neighbour’s bid is crucial (increase by 25%) – e.g. if bid from C would be 0, D should not bit for Y.
The ability to increase the bids by 25% or 50% is important to differentiate between the fact that sth is assigned somewhere else, or if the environment the node knows about includes a bid that can help it’s own bid.
Note this algorithm does not guarantee stability. Also for better results in specific use cases it is encourage to change how the credits are calculated. For example based on the utility of the container node. Especially for the share attribute condition there might be cases that the algorithm does not find the optimal solution, as the increasing percentages (50%, 25%) are not optimal. The time complexity depends on the number of nodes in the container graph, their structure and how often bids & assignment change. This is because currently the container graph is traversed synchronously. In future a async approach would be beneficial, which will also allow for parallel calculation of bids.
The bidding concept is implemented as part of the graph-stitcher tool.
Categories: Personal • Tags: Graph Stitching, Graphs, Python • Permalink for this article
January 2nd, 2016 • Comments Off on Graph stitching
Graph stitching describes a way to merge two graphs by adding relationships/edges between them. To determine which edges to add, a notion of node types is used (based on node naming would be easy :-)). Nodes with a certain type can be “stitched” to a node with a certain other type. As multiple mappings are possible, multiple result/candidate graphs are possible. A good stitch is defined by:
- all new relationships are satisfied,
- the resulting graph is stable and none of the existing nodes (entities) are impacted by the requested once.
So based on node types two graphs are stitched together, and than a set of candidate result graphs will be validated, to especially satisfy the second bullet.
Let’s use an example to explain this concept a bit further. Assume the electrical “grid” in a house can be described by a graph with nodes like the power outlets and fuses, as well as edges describe the wiring. Some home appliances might be in place and connected to this graph as well. Hence a set of nodes describing for example a microwave (the power supply & magnetron), are in this graph as well. The edge between the power supply and the power outlet describe the power cable. The edge between the power supply and the magnetron is the internal cabling within the microwave. This graph can be seen in the following diagram.

(Click on enlarge)
The main fuse is connected to the fuses 1 & 2. Fuse 1 has three connected power outlets, of which outlet #2 is used by the microwave. Fuse 2 has two connected power outlets. Let’s call this graph the container from now on.
Now let’s assume a new HiFi installation (consisting of a blu-ray player and an amplifier) needs to be placed within this existing container. The installation itself can again be described using a simple graph, as shown in the following diagram.

(Click to enlarge)
Placing this request graph into the container graph now only requires that the power supplies of the player and amplifier are connected to the power outlets in the wall using a power cord. Hence edges/relationships are added to the container to stitch it to the request. This is done using the following mapping defition (The power_supply and power_outlet are values for the attribute “type” in the request & container graph):
{
"power_supply": "power_outlet"
}
As there is more than one possible results for stitching two graphs, candidates (there are 2 power supplies and 5 power outlets in the mix) need to be examined to see if they make sense (e.g. the fuse to which the microwave is connected might blow up if another “consumer” is added). But before getting to the validation, the number of candidates graphs should be limited using conditions.
For example the HiFi installation should be placed in the living room and not the kitchen. Hence a condition as follows (The power outlet nodes in the container graph have an attribute which is either set to ‘kitchen’ or ‘living’) can be defined:
condition = {
'attributes': [
('eq', ('bluray_p', ('room', 'living'))),
('eq', ('amp_p', ('room', 'living'))),
]
}
Also the amplifier should not be placed in the kitchen while the blu-ray player is placed in the living room. Hence the four nodes describing the request should share the same value for the room attribute. Also it can be defined that the power supplies of the player & amplifier should not be connected to the same power outlet:
condition = {
'compositions': [
('share', ('room', ['amp', 'amp_p', 'bluray', 'bluray_p'])),
('diff', ('amp_p', 'bluray_p'))
]
}
This already limits the number of candidate resulting graphs which need to validated further. During validation it is determined if a graph resulting out of a possible stitching falls under the definition of a good stitch (see earlier on). Within the container – shown early – the nodes are ranked – red indicating the power outlet or fuse heavy loaded; while green means the power outlet/fuse is doing fine. Now let’s assume no more “consumers” should be added to the second outlet connected to the first fuse as the load (rank) is to high. The high load might be caused by the microwave.
All possible candidate graphs (given the second condition described earlier) are shown in the following diagram. The titles of the graphs describe the outcome of the validation, indicating that adding any more consumers to outlet_2 will cause problems:

(Click to enlarge)
The container and request are represented as shown earlier, while the stitches for each candidate resulting graph are shown as dotted lines.
Graph stitcher is a simple tool implements a simple a stitching algorithm which generates the possible graphs (while adhering all kinds of conditions). These graphs can than be validated further based on different validators. For example by looking at number of incoming edges, node rank like described before, or any other algorithm. The tool hence can be seen as a simple framework (with basic visualisation support) to validate the concepts & usefulness of graph stitching.
Categories: Personal • Tags: Graph Stitching, Python • Permalink for this article



